assignment 5

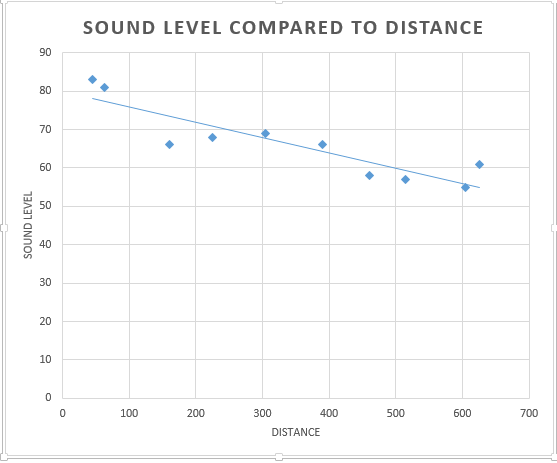
Part 1

The claim that as crime rates increase so does the amount of children receiving free lunches that was made by the news is correct in this statement. When running a regression analysis on these two variables the data suggests that yes there is correlation between the two where with the increase in crime rates there is also a high incidence of free lunches given out to children in schools. But if you look at the r squared value for this relationship it is .173 meaning that the two variables don't really explain each other very well meaning that the relationship is a spurious one. With this analysis one could be 99.5% sure that yes these two variables correlate but the relationship is spurious. Based off this relationship with a crime rate of 79.9 you could expect to have a free lunch percentage of about 40%.

Part 2

Intro

For part two the objective was to examine the enrollment numbers for UW system universities and try to determine if there was a certain variable that could be determined that would cause someone to choose one school over another. thanks to the professor the data of percent with a Bachelors degree, Median Household income and distance each county is from each school. Using this data it is expected to analyze the significance each has on a students university decision.This analysis will require use of regression analysis and mapping of the residuals received from this analysis. To complete these two tasks SPSS is required for the regression analysis and ARCMAP will be used for map creation purposes.

Methods

For this the data for the UW system was provided in a excel file containing broad information about the universities and Wisconsin counties. One of the first things that was done was normalize the population numbers for counties based on the distance from each institution. This is to help decrease the impact that larger counties such as Milwaukee county will have on the results, protecting from possible large outliers. Once this column was created the process of running linear regression analysis could begin. This is a statistical tool that used to evaluate the relationship between two variables often looking for causation in this analysis. This analysis was run three separate times examining the if income education or distance were the largest factor in choice. Each time the dependent variable being number of students attending and the the independent variable being the distance, percent having a bachelors degree or median household income. With these outputs the strength of the relationships could be determined and if they were considered significant or not. Another byproduct of these outputs was the residual creation for each individual county or how far the result for each county is from the best fit line. With these residuals, chloropleth maps could be created showing a visual interpretation of the data.  

Results

Figure 1 population distance for Eau Claire

Figure 2 percent bachelor degree for Eau Claire

Figure 3 Median household income for Eau Claire students

Figure 4 Population distance from county for River Falls

Figure 5 percent bachelors degree for River Falls

Figure 6  Median Household income for River Falls

Figure 7 residual map for Median Household income for River Falls

Figure 8 residual map for population distance for Eau Claire

Figure 9 residual map for percent receiving a Bachelor degree for Eau Claire

For this analysis the schools of UW Eau Claire and UW River Falls were chosen as the study area. Figures one through six are the SPSS outputs for both schools independent variables that were analyzed. The first thing analyzed was the population of the schools coming from each separate county normalized by distance from the institution. For UW Eau Claire the regression analysis produces a significance of .000 meaning that it is almost one hundred percent certain that there is correlation between population of the university and the distance they originate from. This is echoed by the the R square value of .945 so the two variables describe each other very well. This is in stark contrast to the same variables for UW River Falls where the significance of .776 and an R square of .001 meaning that the relationship between the two are neither significant or descriptive of each other. The second variable being examined is the percent of students receiving a Bachelors degree( figures 2 and 5 ). For Eau Claire the significance was .003 and the R Square was .121 meaning that it is a significant relationship between the number of students attending and amount of students receiving a bachelors degree and the two variables do  not describe each other very well. The returns for River Falls were interesting to where the data has a significance of .105 but, for the purposes pf this analysis a significance level of at least 95% is required.  But an interesting part of this return data is that even though the significance level is to high to be considered significant for this the R squared value is .037 meaning that the two variables do not explain each other very well. The final variable that was examined was the Median household income for counties. For Eau Claire the return produces a significance of .104 and an R square value of .037 meaning that the data is about 90% significant but is not significant enough to be relevant for this analysis but the two variables do not explain each other very well. This variable did in fact though describe the data set for River Falls well where it produced a significance of .028 and an R squared of .067.

Conclusions

The goal of this assignment was to determine if there is a variable that could be identified that lead to a students choice in university attended more than usual. The three variables that were examined percent of the county with a bachelors degree, Median Household income of the counties and the total population of the county normalized by the distance from the institution. For  percent of county with a bachelors degree this variable was only truly descriptive for Eau Claire with the low significance and R squared values meaning that the two variables describe each other well. For Median Household income  this seemed to only be a significant relation ship for UW River Falls. For the third variable which is population of county in relation to the distance away from the university was descriptive for UW Eau Claire with the high R square and low significance value. Based on this there is not enough evidence to say that there is one concrete variable that influences the decision of a student to choose a university.Though for each university there is one variable that was examined that was deemed significant in the decision to choose which university in the end it is ultimately the choice of the individual on where they will attend.

Assignment 4

Part 1

D. The hypothesis is that as distance from a given point increases the sound level  decreases.

E. Based solely on the data the hypothesis would be accepted. The data has a correlation of  -.896 menaing that the data has a negative correlation and the trend  line will then be a downward slope. With the correlation of the data being so close to  1 that means that the correlation is a very strong one

2.

In this correlation matrix it is examining the relationships between poverty, ethnicity and whether they walk or not. With this views the areas that are predominately Caucasian  have a strong negative relationship with the below poverty column meaning that for the most part they are not below the poverty line. Though based on this matrix areas that have a significant positive correlation with being below the poverty line, meaning that areas that have a high minority population also have a high incidence of poverty. With the walking column  all races correlate siggnifcantly meaning that there is no assumption that can be made that one race is more prone to walking from this matrix and dataset.

Part 2

Introduction

 With this part of the assignment the task was given to  analyze patterns in voting and turnout for the state of Texas. The output data for this is intended to be presented to the governor to analyze if election patterns have changed over the past 20 years. To do this analysis multiple spatial and statistical analysis programs were required to be used, those being ARCMAP GeoDa and Excel. Some of the ways the data will be anyalyzed is through correlation and spatial auto correlation ( correlation of a variable with itself through space ) analysis. The data that is being analyzed is voter turnout for both the 1980 and 2008 elections, Percent Democratic vote for both the 1980 and 2008 elections and percent Hispanic population for 2010 based on the 2010 census.

Methods 

For analysis the data was provided in the Assignment 4 folder but one section of data required downloading from the US Census website and that was the 2010 Hispanic population data. The shape file was also required to be downloaded from the US census website so the data could be properly connected to the correct counties. The only problem with the data is that the data downloaded from the census was not in the same table as the data that was provided in the assignment 4 folder. The way to fix that problem was to take the percent Hispanic population data from the downloaded data and copy it into a new column within the data that was provided to us in our folders.With these two sets of data and the shape file of Texas counties it was time to utilize ARCMAP. In ARCMAP is where the data tables were joined to the counties shape file based off of the Geo_ID column. Now that the table was joined with the shape file it was ready to by put into GeoDa so that the data could be analyzed using spatial autocorrelation and making a LISA map (Local indicators of spatial autocorrelation)

Results

Figure  1 Percent  Democratic vote 1980 

Figure 2 Percent Democratic vote 1980 LISA 

Figure 3 Percent Democratic vote 2008 

Figure 4 Percent Democratic vote 2008 LISA map

Figure 5 Percent Hispanic population 2010

Figure 6 Percent Hispanic population 2010 LISA map 

Figure 7 Voter turnout 1980

Figure 8 Voter turnout 1980 LISA map

Figure 9 Voter turnout 2008

Figure 10 Voter turnout 2008 LISA map

With election data one of the first things the is helpful to look at is the turnout or where the people voting are actually coming from. This is analyzed with figures seven through ten. Figures seven and eight show the voter turnout for the 1980 election. From the Moran's I it can be see that a majority of the data falls in the center of the plot but there are outlier data value. When looking at the areas of high concentration the high voter turnout is generally located in the north of Texas  and the areas of low voter turnout are located to the south of the state. The same trend can be said for the the 2008 election though there is a visible shift here with the areas that are high and low voter turnout seemingly decreasing  or shifting with the areas that were previously low voter turnout in the south of Texas beginning to trend to a higher turnout. The opposite can be said for the north where high voter turnout was previously found with those areas becoming normalized or shifting to a low high correlation. The second big thing to examine is what party these voter are casting their ballots for. Historically Texas is know as a republican state, and examining figure one confirms that with the areas of high democratic votes being minimal and the areas a of low democratic votes being very high. But comparing it to the 2008 data another interesting comparison can be made though the amount of counties that were before considered to be strong republican voting counties may be the same the number of counties that are voting strong democrat are actually increasing. This is really important when comparing it to voter turn out since in the LISA map for the 2008 election shows that the areas that are beginning to trend to being high voter turn out counties are also the counties that are voting predominantly democrat. Through all this analysis there has been a visible shift in voting trends in the state of Texas. Voter Turnout has begun shifting with norther counties decreasing their presence at the polls with southern  counties begining to turn out more. The other big trend shift is the shift from Texas being a predominantly republican voting state to a more well balanced with a rising democratic vote.

conclusions

With this assignment the requirement was to examine Texas voter data for the 1980 and the 2008 elections at the county level. The task was to interpret this data and determine whether any trends are developing noticeably in both voter turnout and which party the vote is cast for. Programs Such as ARCMAP and GeoDa were utilized to compile the data and create LISA maps for the data analysis. Through this data analysis visable trend emerged in the 1980 election  high voter turnout was in the north and low turn out was in the south. democratic voters were concentrated in the south. Though  in the 2008 election  these patterns seemed to start to switch with voter turnout in the north deminishing and the south beginning to increase. This means that potentially Texas could become a state that has a higher proportion or democratic voters than republican if these trend were to continue.

Assignment 2

The goal of this exercise was to examine the geography behind severity of Tornadoes in Oklahoma and Kansas. Through this exercise two time periods were examined, Tornado Locations and width of tornadoes from 1995-2006 and also from 2007-2012. We were asked the question of should the people that live in these high tornado prone areas be required to build shelters or would it just be a waste of resources? Are there areas where you are more prone to having tornadoes occur? Another aspect of this job was also to analyze if a significant change has occurred or not between these two time periods in both location and size of tornado incidences.  

The data that was utilized was point data for the locations of tornadoes in Oklahoma and Kansas. Each point of data also carried with it the width of the tornado and for this assignment it was assumed the width was directly related to the severity, so the larger the width the more severe the tornado. The time period of this data stretched from 1995 to 2012 and was broken into two separate sets of data.  For calculations it was required that ARCMAP was utilized, this made short work of the analysis of the main components of the exercise. From there the maps were exported to Adobe Illustrator to be cleaned and finished before being exported as a final product, one of these main components of this analysis was the calculation of statistics that heavily relate to these data sets such as the standard deviation, z-score, mean center and the standard distance of the point data. The mean center of the data is a spatial measure of the central tendency of the data or where the center of the data would lie if it was a point on a Cartesian plane.  This is essentially a way of spatially visualizing the mean of the data to put meaning to numbers. Something similar that is examined in this lab is the weighted mean center. Like the mean center it is a spatial representation of the mean of the data but is weighted by the frequency of the data. An example of this would be either Figure 1, 2 or 3 where both the mean center and the weighted mean center are displayed on the same map. It is easily visible that the two points are located in different positions on the map. Another one of the main components of this lab was the visualization of standard distance which is just the way to spatially show the standard deviation of the data.

From this analysis of the data sets there is significant argument for the construction of these severe weather shelter due to many factors. As is visible in figures 1 and 2

Figure 1

Figure 2

the distribution of the tornado location themselves are fairly evenly distributed. This is echoed by examining the placement of the mean center on each of these maps which lies fairly central within the two states. Though for severity of tornado the weighted mean center was utilized. This weighting of the data draws the mean center further south showing that more severe tornadoes occur in Oklahoma than Kansas. Another main component to this exercise was to determine if there had been significant change in severity and location of tornadoes occurring. In the time period from 1995-2006 most of the severe tornadoes were located in Oklahoma which when looking at the weighted mean center is what dragged the point south for that data set. Though from observing figures 4 and 5 it is

Figure 4

Figure 5

evident that even though the mean center itself is being pulled southeast due to the higher amount of tornadoes occurring a vast majority of the data still falls within 1 standard distance of the mean center. From the analysis it can be assumed that if these trends were to continue then 70% of the time there will be 2 tornadoes that occur (rounded from 1.764) and 20% of the time 8 will occur (rounded from 7.612). In this exercise another task was to calculate the z scores for counties and how many tornadoes occur in them. It was required to calculate this for 3 separate counties, Russel KS, Cado OK, and Alfalfa OK. The z scores were as follows Russel: 4.8837, Cado: 2.0930 and Alfalfa: 0.2326 these are visible in figure 7

Figure 7

which is the chloropleth map of standard deviations for the number of tornadoes occurring in the Oklahoma and Kansas counties. Russel County here is on the higher end though is not the highest value in the data set. The Z score being abnormally high indicates that there is a large amount of tornadoes actually occurring in this given county.

In this exercise the task of using the datasets provided to determine whether it would be rational to require the construction of severe weather shelters in Oklahoma and Kansas. Though this analysis things such as mean, mean center, standard distance and Z score were examined to answer this research question. It was clear that in the first data set the tornado locations were concentrated in south eastern Oklahoma which drew the weighted mean center south east. But as time went on the amount and severity of the tornadoes trended towards occurring in Kansas which dragged the mean center and weighted mean center for that data set north and northwest respectively.  This means that even though the location and severity of the tornadoes may have shifted the fact that the amount of tornadoes is still very high remains. Therefore I would suggest that people would build these severe storm shelters but not make it a requirement. I would especially suggest this if the citizens lived within 1 standard distance of the mean center because the likelihood of a tornado occurring there is much higher.

Figure 3

Figure 7